Allan方差分析法分析静态噪声的原理及实例代码

发表于 更新于 分类于

本文给出了 Allan 方差的计算方法，应用于噪声分析的原理、步骤，并在结尾附上了计算函数的代码和应用实例。

Allan 方差

Allan方差分析法分析惯性仪器（本文以陀螺仪为例）静态噪声的原理：将不同噪声的功率谱密度函数转换为 Allan 方差表达式，分析它们噪声在 Allan 方差曲线上的特定斜率，并在陀螺仪测量数据计算出的 Allan 方差曲线上进行匹配，再根据特征点求解每种噪声成分的系数。

Allan 方差 (Allan Variance, AVAR)，中文一般称为阿仑方差

Allan 方差一般能识别以下五种噪声：

  • 量化噪声
  • 角度随机游走噪声
  • 零偏不稳定性
  • 角速率随机游走噪声
  • 速率斜坡

分析步骤

  1. 采集陀螺仪静态噪声

  2. 根据噪声信号计算并画出出 Allan 方差曲线

  3. 在 Allan 方差曲线匹配每种噪声的特征斜率，根据函数与图像关系找到特征点，求出每种噪声的功率谱密度函数种的系数

五种噪声分析

功率谱密度函数与 Allan 方差之间的关系：

$$
\sigma _ {y} ^ 2 (\tau) = 4 \int_{0}^{\infty} S _ {y}(f) \frac{\sin^4(\pi f \tau)} {(\pi f \tau)^2} df
$$

将噪声的功率谱密度函数代入上式，即可得到噪声的 Allan 方差表达式，最后取双对数分析。

噪声类型 功率谱密度 Allan 方差 特征斜率 特征点
量化噪声(QN) $S_ {\Delta}(f) = \tau_{\tiny0}Q^2$ $\log_{10}\sigma_{\tiny{QN}}(\tau)=\log_{10}\sqrt{3}Q-\log_{10}\tau$ -1 $(1,\sqrt{3}Q)$
角度随机游走(ARW) $S_{\varOmega}(f) = N^2$ $\log_{10} \sigma_{\tiny{ARW}}(\tau) = \log_{10}N - \frac{1}{2}\log_{10}\tau$ $-\frac{1}{2}$ $(1,N)$
零偏不稳定性噪声(BI) $S_{\varOmega}(f) = \frac{B^2}{2 {\pi} f}$ $\log_{10} \sigma_{\tiny{ARW}}(\tau) = \log_{10}\frac{2B}{3}$ 0 $(1,\frac{2B}{3})$
角速率随机游走（RRW） $S_{\varOmega}(f) = \frac{K^2}{(2 {\pi} f)^2}$ $\log_{10} \sigma_{\tiny{ARW}}(\tau) = \frac{1}{2}\log_{10}\frac{K}{\sqrt{3}}$ $\frac{1}{2}$ $(1,\frac{K}{\sqrt{3}})$
速率斜坡(RR) - $\log_{10} \sigma_{\tiny{ARW}}(\tau) = \log_{10}\frac{R\tau}{\sqrt{2}}$ 1 $(1,\frac{R}{\sqrt{2}})$

注：对于速率斜坡噪声，一般假设角速率 $\Omega$ 与测试时间 t 之间呈线性关系$\varOmega(t) = \varOmega(0) + Rt$，Allan 方差可直接计算

Allan 方差计算过程

输入：角速率序列，取样时间为 $\tau_{0}$

输出：不同相关时间$\tau$下的 Allan 方差值，并取双对数绘制成 Allan 方差曲线

下面是具体的计算步骤：

  1. 首先计算取样时间为 $\tau_{\tiny0}$ 时的 Allan 方差：

$$
\hat{\sigma}^{2} _ {A}(\tau_{\tiny0}) = \dfrac{1}{2 (N-1)}\textstyle\sum_{k=1}^{N-1}[\overline{\varOmega} _ {k+1}(\tau_{\tiny0}) - \overline{\varOmega} _ {k}(\tau_{\tiny0})]^2
$$

  1. 其次将取样时间间隔加倍，记 $\tau_{\tiny1} = 2^1 \tau_{\tiny0}​$ 和 $N_{1} = [N/2]​$（$[\enspace \cdot \enspace]​$ 表示取整），在相继奇偶序号角速率之间作算术平均，即
    $$
    \overline{\varOmega} _ {k} (\tau_{\tiny1}) = \dfrac{\overline {\varOmega} _ {2k-1} (\tau _ {\tiny0}) + \overline {\varOmega} _ {2k} (\tau _ {\tiny0})} {2}, \quad k = 1,\enspace 2,\enspace 3,…,\enspace N _ {1}
    $$
    组成新的取样时间间隔为 $\tau{\tiny1}$ 的平均角速率序列，即
    $$
    \overline{\varOmega} _ {1} (\tau _ {\tiny1}), \enspace \overline{\varOmega} _ {2} (\tau _ {\tiny1}), \enspace \overline{\varOmega} _ {3} (\tau _ {\tiny1}), \enspace …, \enspace \overline{\varOmega} _ {N _ 1} (\tau _ {\tiny1})
    $$
    显然新序列长度减半（但可能相差 1 个数据，下同），计算取样时间为 $\tau _ {\tiny1}$ 时的 Allan 方差，即
    $$
    \sigma _ {A} ^ 2 (\tau _ {\tiny1}) = \dfrac {1} {2(N _ 1-1)} \textstyle\sum _ {k=1} ^ {N _ 1-1} [\overline{\varOmega} _ {k+1} (\tau _ {\tiny1}) - \overline{\varOmega} _ {k}(\tau _ {\tiny1})]^2
    $$

  2. 再次将取样时间间隔加倍，记 $\tau _ {\tiny2} = 2 \tau _ {\tiny1} = 2 ^ 2 \tau _ {\tiny0}$ 和 $N _ {2} = [N _ {1} / 2]$，计算平均角速率，即
    $$
    \overline{\varOmega} _ {k} (\tau_{\tiny2}) = \dfrac{\overline {\varOmega} _ {2k-1} (\tau _ {\tiny1}) + \overline {\varOmega} _ {2k} (\tau _ {\tiny1})} {2}, \quad k = 1,\enspace 2,\enspace 3,…,\enspace N _ {2}
    $$
    组成新的取样时间间隔为 $\tau{\tiny2}$ 的平均角速率序列，即
    $$
    \overline{\varOmega} _ {1} (\tau_{\tiny2}), \enspace \overline{\varOmega} _ {2} (\tau _ {\tiny2}), \enspace \overline{\varOmega} _ {3} (\tau _ {\tiny2}), \enspace …, \enspace \overline{\varOmega} _ {N _ 2} (\tau _ {\tiny2})
    $$
    新序列的长度再次减半，计算取样时间为 $\tau _ {\tiny2}$ 时的 Allan 方差，即
    $$
    \sigma _ {A} ^ 2 (\tau _ {\tiny2}) = \dfrac {1} {2(N _ 2-1)} \textstyle\sum _ {k=1} ^ {N _ 2-1} [\overline{\varOmega} _ {k+1} (\tau _ {\tiny2}) - \overline{\varOmega} _ {k}(\tau _ {\tiny2})]^2
    $$

  3. 如此反复将取样时间间隔不断加倍，记 $\tau _ {\tiny{L}} = 2 \tau _ {\tiny{L-1}} = 2^{L} \tau _ {\tiny{0}}$ 和 $N _ L = [N _ {L-1}/2]$，直至最终序列的长度不大于2，得平均角速率序列为
    $$
    \overline{\varOmega} _ {1} (\tau_{\tiny{L}}), \enspace, \enspace\overline{\varOmega} _ {N _ L} (\tau _ {\tiny{L}})
    $$
    并计算取样时间为 $\tau _ {\tiny{L}}$ 时得 Allan 方差，即
    $$
    \sigma _ {A} ^ 2 (\tau _ {\tiny{L}}) = \dfrac {1} {2(N _ L-1)} \textstyle\sum _ {k=1} ^ {N _ L-1} [\overline{\varOmega} _ {k+1} (\tau _ {\tiny{L}}) - \overline{\varOmega} _ {k}(\tau _ {\tiny{L}})]^2
    $$
    至此，获得一系列得点对 $\tau _ {\tiny{i}} \backsim \sigma _ {A} ^ 2 (\tau _ {\tiny{i}})$ 或 $\tau _ {\tiny{i}} \backsim \sigma _ {A} (\tau _ {\tiny{i}}), \enspace i=1, \enspace 2, \enspace 3, \enspace … L$，完成 Allan 方差估计，并将结果绘制成双对数图。

注意事项：

  1. Allan Variance 与 Allan Deviation

    虽然我们称这种分析方法为 Allan 方差 $\tau_{\tiny{i}} \backsim \sigma _ {A} ^ 2 (\tau _ {\tiny{i}})$，但是在实际分析时一般取根号，得到的是 Allan Deviation $\tau _ {\tiny{i}} \backsim \sigma _ {A} (\tau_{\tiny{i}})​$

  2. 只能用于静态噪声分析

    Allan 方差滤波器在零频率处截止，因此基座常值角速率干扰并不影响 Allan 方差的计算结果，但基座变角速率会引起额外的功率谱分量，如果不能消除会影响陀螺 Allan 方差性能参数分析的准确性。

  3. 单位转换问题

    国际单位制，$\tau$ 和 $\sigma_{A}(\tau)$ 的单位分别取 $rad/s$ 和 $s$，但实际分析过程中一般 $\sigma$ 常以 $^\circ/h$ 为单位，并且各项噪声系数也常使用 $^\circ​$ 和 $h$ 的组合作为单位（除 Q 外），所以，求噪声系数的特征点也会随之改变，这里特征点的横坐标单位为 $s$。

噪声类型 误差系数 习惯单位 特征斜率 特征点
量化噪声(QN) Q “ -1 (1, $\sqrt{3}Q$)
角度随机游走(ARW) N $^\circ/h^{\frac{1}{2}}$ $-\frac{1}{2}$ (100, 6N)
零偏不稳定性噪声(BI) B $^\circ/h$ 0 (1, $\frac{2B}{3}$)
角速率随机游走（RRW） K $^\circ/h^{\frac{3}{2}}$ $\frac{1}{2}$ (100, $\frac{K}{6\sqrt{3}}$)
速率斜坡(RR) R $^\circ/h^2$ 1 (1000, $\frac{R}{3.6\sqrt{2}}$)

代码实现

实例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
% 传感器: MEMS陀螺仪
% 采样频率：1000 Hz
% 采样时间：2.5 h
clear all; clc; close all;
load('G:\Code\Matlab\Allan\1000Hz-3h-01.mat');
data = all_mixed.data{1,3};
data = (data - 2.5) * 1000 / 20;
Y = data'; % 转换为列向量
dt =1/1000;  %s 采样周期设定
[AllanSigma, T] = AllanCompute(Y,dt);

AllanSigma = AllanSigma*3600; % 转换 Allan 方差单位 to deg/h
T = T/3600; % 转换时间单位 to h
slopes = [-1;-0.5;0;0.5;1];
Ts = [sqrt(3);1;NaN;3;sqrt(2)];

plot = 1;
method = 2; % 使用最短路径匹配斜率
[sigmasOut,figs,hs] = AllanAnalyze(AllanSigma,T,slopes,Ts,plot,method);
NoiseAnalyze(sigmasOut, figs, hs);

求得的 Allan 方差曲线图和斜率图如下：

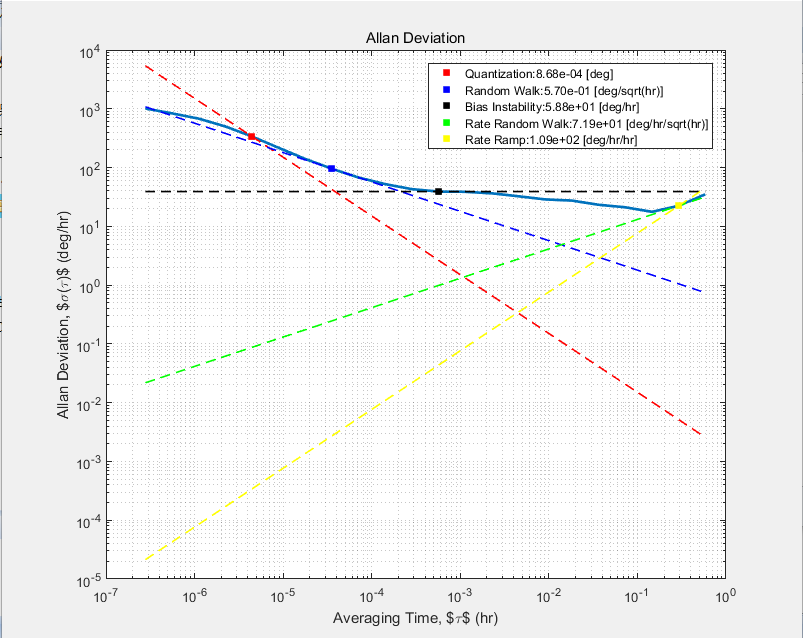
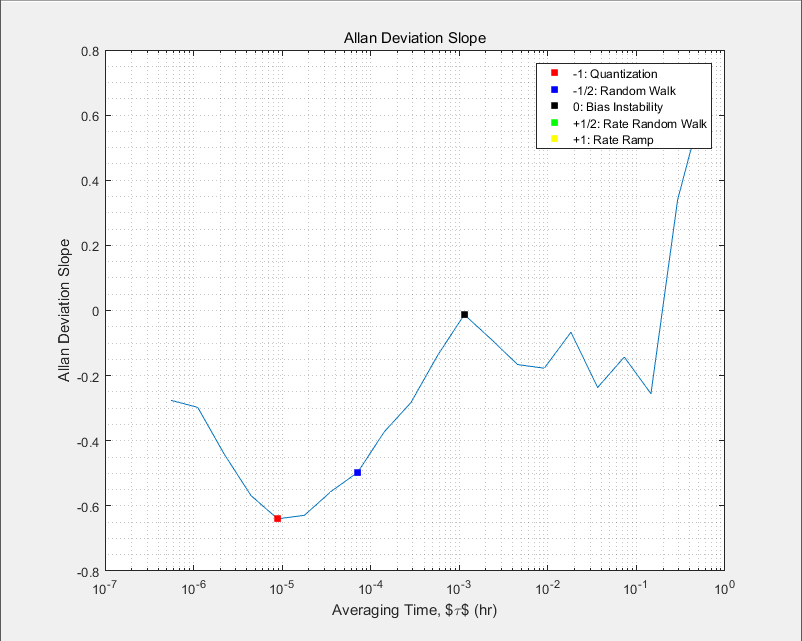
下面是函数 AllanCompute, AllanAnalyze, NoiseAnalyze 的源码：

AllanCompute.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function [sigma, tau, Err] = AllanCompute(y0, tau0)
% 计算Allan方差
% 输入：y -- 静态采集的数据(一行或列向量); tau0 -- 采样周期,单位：s
% 输出：sigma -- Allan Deviation(量纲单位与输入y保持一致), tau -- 取样时间, Err -- 百分比估计误差
% 作者: Yan Gong-min, 2012-08-22
% example: 
%     y = randn(100000,1) + 0.00001*[1:100000]';
%     [sigma, tau, Err] = avar(y, 0.1);
    N = length(y0);
    y = y0; NL = N;
    for k = 1:inf
        sigma(k,1) = sqrt(1/(2*(NL-1))*sum([y(2:NL)-y(1:NL-1)].^2));
        tau(k,1) = 2^(k-1)*tau0;
        Err(k,1) = 1/sqrt(2*(NL-1));
        NL = floor(NL/2);
        if NL<3
            break;
        end
        y = 1/2*(y(1:2:2*NL) + y(2:2:2*NL));  % 分组长度加倍(数据长度减半)
    end

AllanAnalyze.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
function [sigmasOut,f,h] = AllanAnalyze(AD,T,Slopes,Ts,plots,method)
%根据计算结果画出 Allan 方差曲线，求出噪声系数：
% OUPUT
% sigmasOut: 计算求得的每种噪声的系数
% f: 输出的图形句柄序列：f(1) 为 Allan 方差曲线，f(2) 为斜率曲线
% h: axis handles to plotted elements
%
% INPUT：
% AD: 计算出的 Allan Deviation，单位: deg/h.
% T: 相关时间序列，单位 h.
% Slopes: 每种噪声的特征斜率
% Ts: 用于代入到斜率直线求噪声系数的横坐标序列
% plots: 是否画图
% method: 匹配斜率的方法，1为最先匹配法，2为最短路径匹配（优选2）


% 确保每个斜率都有对应的 Ts
if length(Slopes)~=length(Ts)
    error('Each slope must have a corresponding Ts. Enter NaN if no Ts')
end

% 计算出 Allan 方差曲线的斜率序列
% slope is: (Log10(Y(t+1))-Log10(Y(t)))/((Log10(X(t+1))-Log10(X(t)))
slope = logdiff(AD)./logdiff(T);

% 画图
if plots
    h = zeros(2,length(Slopes)+1);
    f(1) = figure;
    h(1,1) = loglog(T,AD,'LineWidth',2); hold on;
    title('Allan Deviation')
    xlabel('Averaging Time');
    ylabel('Allan Deviation');
    f(2) = figure;
    h(2,1) = semilogx(T(2:end),slope); hold on;
    title('Slope of Allan Deviation');
    xlabel('Averaging Time');
    ylabel('Log-Log Slope');
    
    % Color string for marking up each slope of interest in figures
    c = {'r';'b';'k';'g';'y'};
else
    h = 0;
    f = 0;
end

% Creaate output vector shell
sigmasOut = zeros(length(Slopes),1);

% Now, step through each slope of interest, find the slope in the Allan
% deviation signal, extrapolate to corresponding Ts of interest and record
% the coefficient found at that location.
for ii = 1:length(Slopes)
        curr_slope = Slopes(ii);
        curr_t = Ts(ii);
        
        % Method 1: Use knowledge of Allan deviation shape, starting from
        % the left (small T), look for first occurence of desired slope.
        % Method 2: Use min distance method to locate point with closest
        % matching slope to the one desired.
        if method==1
            if sign(slope(1)) == -1 % 判断斜率如果为负
                idx = find(slope>curr_slope,1,'first'); % 第一个斜率大于 slope 的位置
            else
                idx = find(slope<curr_slope,1,'first');
            end
        elseif method==2 % 方法2，最短路径匹配，找到与特征斜率最接近的斜率在曲线种所处的位置
            dist = (slope-curr_slope).^2;
           [~,idx] = min(dist);
        end

        % 根据曲线特征斜率点创建直线函数，代入 Ts，求解噪声系数
        if ~isempty(idx)
            if isnan(curr_t)
                sigmasOut(ii) = AD(idx);
                linefun = @(t) AD(idx) + 0*t;
            else
                linefun = @(t) 10.^(curr_slope*(log10(t)-log10(T(idx)))...
                    +log10(AD(idx)));
                sigmasOut(ii) = linefun(curr_t);
            end

            if plots
                figure(f(1)); h(1,ii+1) = plot(T(idx),AD(idx)...
                    ,'s','Color',c{ii},'MarkerFaceColor',c{ii});...
                    plot(T,linefun(T),'--','LineWidth',1.2,'Color',c{ii});
                figure(f(2)); h(2,ii+1) = plot(T(idx+1),...
                    slope(idx),'s','Color',c{ii},'MarkerFaceColor',c{ii});
            end
        end
end

% 用于双对数曲线求斜率
function logdiff = logdiff(X)
N = size(X,1);
logdiff = zeros(N-1,1);
for ii = 1:N-1
    logdiff(ii) = log10(X(ii+1))-log10(X(ii));
end

NoiseAnalyze.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
function [] = NoiseAnalyze(sigmasOut, figs, hs)
% 在图中标出噪声并打印到命令行窗口
sigmasOut(3) = sigmasOut(3)/sqrt((2*log(2)/pi));


fprintf(' Quantization:%0.2e [deg]\n', sigmasOut(1));
fprintf('Random Walk:%0.2e [deg/sqrt{hr}]\n',sigmasOut(2));
fprintf('Bias Instability:%0.2e [deg/hr]\n',sigmasOut(3));
fprintf( 'Rate Random Walk:%0.2e [deg/hr/sqrt{hr}]\n', sigmasOut(4));
fprintf( 'Rate Ramp:%0.2e [deg/hr/hr]\n', sigmasOut(5));

% sigmasOut(1) % Quantization  deg (gyros) OR m/s (accels)
% sigmasOut(2) %  Random Walk  deg/sqrt(hr) (gyros) OR m/s/sqrt(hr) (accels)
% sigmasOut(3)%  Bias Instability  deg/hr (gyros) OR m/s/hr (accels)
% sigmasOut(4)% Rate Random Walk deg/hr/sqrt(hr) (gyros) OR m/s/hr/sqrt(hr)(accels)
% sigmasOut(5) % Rate Ramp deg/hr/hr
sigmaQ = sprintf('Quantization:%0.2e [deg]',...
    sigmasOut(1));
sigmaRW = sprintf('Random Walk:%0.2e [deg/sqrt(hr)]',...
    sigmasOut(2));
sigmaBias = sprintf('Bias Instability:%0.2e [deg/hr]',...
    sigmasOut(3));
sigmaRRW = sprintf(...
    'Rate Random Walk:%0.2e [deg/hr/sqrt(hr)]',...
    sigmasOut(4));
sigmaRR = sprintf(...
    'Rate Ramp:%0.2e [deg/hr/hr]',...
    sigmasOut(5));
figure(figs(1)); hold on; title('Allan Deviation');
set(gcf,'Position',[0 0 800 800]);
legend(hs(1,2:end),sigmaQ,sigmaRW,sigmaBias,sigmaRRW,sigmaRR,'Location',...
    'NorthEast');
xlabel('Averaging Time, $\tau$ (hr)');
ylabel('Allan Deviation, $\sigma(\tau)$ (deg/hr)');
grid minor;


figure(figs(2)); hold on; title('Allan Deviation Slope');
set(gcf,'Position',[0 0 800 800]);
legend(hs(2,2:end),'-1: Quantization','-1/2: Random Walk',...
    '0: Bias Instability','+1/2: Rate Random Walk',...
    '+1: Rate Ramp','Location','NorthEast');
xlabel('Averaging Time, $\tau$ (hr)');
ylabel('Allan Deviation Slope');
grid minor;

参考资料

[1]: 惯性仪器测试与数据分析, 135-158